ჟურნალის წინა ნომერში გამოქვეყნებული
ამოცანა #114:
კლასში 30 მოსწავლეა. თითოეულ მათგანს ჰყავს თანაკლასელთა შორის ერთი და იგივე რაოდენობის მეგობარი. მოსწავლეს ვუწოდოთ ბეჯითი, თუ ის თავის მეგობრებიდან უმრავლესობაზე უკეთესად სწავლობს. მაქსიმუმ რამდენი ბეჯითი მოსწავლე შეიძლება იყოს კლასში? (ითვლება, რომ ნებისმიერი ორი მოსწავლისთვის შესაძლებელია ითქვას, თუ რომელი სწავლობს უკეთესად).
ამოცანის პასუხი:
ვთქვათ, x არის კლასში ბეჯით მოსწავლეთა რაოდენობა, ხოლო k-თი აღვნიშნოთ თითოეული მოსწავლის მეგობრების რაოდენობა. სულ მეგობარი წყვილების რაოდენობაა
1 (ყველაზე ბეჯითი) მოსწავლე სწავლობს თავისი k მეგობრიდან ყველაზე უკეთ, ხოლო ყველა დანარჩენი x-1 ბეჯითი მოსწავლე სწავლობს არანაკლებ [k/2]+1 მეგობარზე უკეთ. (კვადრატული ფრჩხილები აღნიშნავს რიცხვის მთელ ნაწილს. მაგალითად [12,5]=12). ცხადია
გამოდის, რომ სულ ბეჯითი მოსწავლეები არიან უკეთესები სწავლაში არანაკლებ
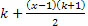 ცალ წყვილში. ცალ წყვილში. |
|
|
რადგან მეგობარი წყვილების რაოდენობაა
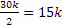 , ე.ი. გვაქვს უტოლობა: , ე.ი. გვაქვს უტოლობა:
|
|
|
ანუ
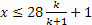 |
|
(1)
|
შევნიშნოთ, რომ
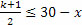 |
|
(2)
|
რადგან იმ მოსწავლეთა რაოდენობა, ვისზე უკეთესადაც სწავლობს ბეჯითებს შორის ყველაზე უარესი, არ აღემატება (30-x)-ს.
(1) უტოლობის მარჯვენა მხარე იზრდება k-ს ზრდასთან ერთად. (2) უტოლობა გადაიწერება ასე:
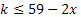 |
|
(3) |
(1) და (3) უტოლობებიდან ვღებულობთ:
საიდანაც
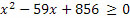 |
|
(4) |
უდიდესი მთელი რიცხვი, რომელიც აკმაყოფილებს (4) უტოლობას და x<30 პირობას, არის x=25. გამოდის, რომ ბეჯითი მოსწავლეების რაოდენობა არ აღემატება 25-ს. ახლა მოვიყვანოთ ისეთი მაგალითი, როცა ბეჯითი მოსწავლეების რაოდენობა არის ზუსტად 25.
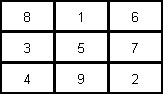
დავნომროთ მოსწავლეები 1-დან 30-მდე რიცხვებით. შემდეგ დავალაგოთ "უკეთესობის" კლებადობის მიხედვით (1-ლი ყველაზე უკეთ სწავლობს, 30-ე - ყველაზე ცუდად) და ჩავსვათ ქვემოთმოყვანილ ცხრილში შემდეგნაირად:
ჩავთვალოთ, რომ მოსწავლეები არიან მეგობრები, თუ მათი შესაბამისი ნომრები მდებარეობენ:
ა) მეზობელ სტრიქონებში და განსხვავებულ სვეტებში;
ან - ბ) ერთსა და იმავე სვეტში და ამასთან, ერთ-ერთი მათგანი მდებარეობს ბოლო სტრიქონში;
ან - გ) პირველ სტრიქონში.
ამ მაგალითში თითოეულ მოსწავლეს ჰყავს 9 მეგობარი. პირველი 25 მოსწავლიდან თითოეული სწავლობს მინიმუმ 5 თავის მეგობარზე უკეთ.
ამგვარად, მაქსიმალური რაოდენობა ბეჯითი მოსწავლეებისა არის 25.
ამჯერად ჟურნალის მკითხველებიდან სწორი პასუხი ვერავინ გვაცნობა.
მორიგი
ამოცანა #115:
კვადრატი დაყოფილია უჯრებად (იხ. სურათი). თითოეულ უჯრაში ჩაწერილია სხვადასხვა რიცხვები 1-დან 9-მდე, ისე რომ თითოეულ სვეტში, სტრიქონში და დიაგონალზე მათი ჯამი ერთი და იმავე რიცხვის ტოლია. ასეთ კვადრატს
 |
|
"მაგიურ კვადრატს" უწოდებენ. არსებობს თუ არა მაგიური კვადრატი, რომელიც
შევსებულია ნატურალური რიცხვების შებრუნებული რიცხვებით? (მაგალითად, 7-ის
შებრუნებული რიცხვი არის წილადი 1/7). |
პირველ მკითხველს, ვინც სწორად უპასუხებს ამ ამოცანას, გადაეცემა შესანიშნავი საჩუქარი - შპს "ააფ მენეჯმენტის" მიერ გამოცემული ერთ-ერთი წიგნი:
1) ფრანგი მწერლის, ნობელის პრემიის ლაურეატის ანდრე ჟიდის რომანი
"ვიწრო კარიბჭე";
2) ო. ჰენრის ნოველების კრებული
"ზაფხულის შუადღის სიზმარი";
3) ფრანგი მწერლის, რეიმონ კენოს რომანი
"ქალი არ უნდა გაანებივრო".
გამარჯვებულის ვინაობა გამოქვეყნდება! დაგვირეკეთ ტელეფონზე: (95)-59-02-75.
გისურვებთ წარმატებებს!
ფრიდონ ალშიბაია

